– eine virtuelles Arbeitsmittel zur Erkundung der Addition und Subtraktion im Zahlenraum bis 20.
Auf Grundlage der Erkenntnisse bei der Beobachtung von Kindern bei der Bearbeitung von mathematischen Lernsoftwareübungen sind viele Ideen für die Realisation und lernunterstütztenden Gestaltung von virtuellen Arbeitsmitteln entstanden. Einige davon habe ich in einem virtuelles Zwanzigerfeld umgesetzt. Das Arbeitsmittel ist für mich vor allem auch ein Forschungswerkzeug, wie virtuelle Handlungsangebote so gestaltet werden können, dass sie das mathematische Verstehen beim Kind befördern. Ich freue mich deshalb auch über Erfahrungsberichte und Anregung zur Weiterentwicklung.
Bitte beachten: Da die Flash-Technologie ausgelaufen ist und zukünftig nicht mehr funktionieren wird, musste die App neu programmiert werden. Die neue App Rechenfeld deckt den Funktionsumfang der App ab und erweitert sie.
Das Zwanzigerfeld ist so konzipiert, dass es als Erweiterung und Fortführung zu der Arbeit mit dem gegenständlichen Zwanzigerfeld eingesetzt werden sollte für Kinder, die noch Schwierigkeiten beim Legen und Übertragen der Darstellungen haben. Es bietet dafür „didaktische Mehrwerte„, z.B. die interaktive Verknüpfung von Handlungen an ikonischer (z.B. Wenden von Plättchen) und symbolischer Repräsentationsebene (Veränderung der Rechenaufgabe).
Bislang bietet das virtuelle Zwanzigerfeld folgende Handlungsmöglichkeiten (vgl. Video):
- Plättchen lassen sich wenden (Klick auf den Rechenstein), einfügen und löschen. Dabei werden die Handlungen als Animationen angezeigt und es können die Auswirkungen der Handlungen auf der symbolischen Aufgabendarstellung als Additionsaufgabe beobachtet werden.
- Beim Klick auf eine Zahlziffer wird die entsprechende Menge im Zwanzigerfeld durch ein kurzes Blinken hervorgehoben. Damit wird die Beziehung zwischen Zahlen in der Aufgabe und Menge visuell verdeutlicht und die Menge kann besser auf einen Blick erfasst werden (quasi-simultane Mengenerfassung).
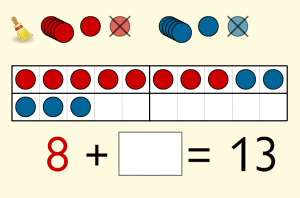
- ein „Abdeckung“ für einzelne Zahlziffern. Es steht ein Rechteck zur Verfügung, mit dem man beliebige Zahlziffern abdecken und so verschiedene Aufgabentypen entstehen lassen kann (z.B. 5 + _ = 12 oder 5 + 7 = _). Das Ergebnis kann selbst kontrolliert werden, indem das Abdeckrechteck wieder weggeschoben wird.
- Einfügen der Mengen in Fünferportionen entsprechend der „Kraft der Fünf“ (Klick auf Fünferstapel).
- Die Zahlziffern lassen sich über die Pfeile (sie erscheinen bei Klick auf die jeweilige Zahlziffer) um Eins erhöhen oder veringern und die Auswirkungen auf die Menge im Zwanzigerfeld können simultan zu dieser Handlung beobachtet werden (Übertragung von symbolischer zur ikonischer Ebene).
- Es lässt sich über den Button links unten zwischen einer linearen Anordnung der Plättchen (10er-Reihe wird zuerst mit Plättchen aufgefüllt, bevor eine neue Reihe begonnen wird) und einer Anordnung untereinander (rote Plättchen in der oberen Reihe, blaue Plättchen in der unteren Reihe) umschalten und so unterschiedliche Darstellungen einer Aufgabe realisieren, die für unterschiedliche Rechenstrategien unterstützend genutzt werden können.
- Gelegte Aufgaben im Zwanzigerfeld lassen sich „abspeichern“ (über das Fotosymbol) und bis zu 10 gespeicherte Aufgaben auf einer Seite ausdrucken (über das dann eingeblendete Druckersymbol). So lassen sich Lernprozesse bei der Arbeit mit dem Zwanzigerfeld dokumentieren und gelegte Aufgaben können für die Kommunikation und Reflexion darüber „offline“ genutzt werden. Zudem lässt sich diese Funktion auch als Aufgabenblatt-Generator für den Lehrer nutzen.
- Eine Umschaltung zwischen Plus- und Minusaufgaben über einen Button. So lassen sich beide Grundoperationen auf einem Feld legen und Bezüge zwischen Addition und Subtraktionsaufgaben hergestellt werden. So können beispielsweise Umkehraufgaben veranschaulicht und erfahrbar gemacht werden (z.B. 5+4 = 9 wird zu 9-4 =5).
- Bei Aufgaben mit Zehnerübergang wird die Zerlegung des zweiten Summanden automatisch angezeigt und so die Entwicklung der Zerlegungsstrategie unterstützt. Mehr dazu in einem gesonderten Beitrag über den Zehnerübergang. Diese Funktion lässt sich über einen Button links unten aus- und wieder einschalten.
- Es lassen sich die Aufgaben durch den Veränderungs-Button vom Programm verändern. Dabei wird per Zufallsmodus ausgewählt, ob ein oder 10 Plättchen gewendet, hinzugefügt oder weggenommen werden oder die Tauschaufgabe angezeigt wird. Diese Funktion lässt sich verwenden, um operative Bezüge zwischen Aufgaben zu entdecken (Was hat sich verändert? Wie ändert sich dann das Ergebnis? usw.) im Sinne operativen Übens.
- Noch Experimentell ist die Integration einer Eingabefunktion auf dem Abdecker. So lassen sich Lösungsvorschläge direkt auf dem Abdecker eingeben und später selbst kontrollieren. Diese Eingabefunktion kann durch Drücken der Taste „g“ ein- und ausgeblendet werden.
In einem kurzen Video werden einige grundlegende Funktionen des Zwanzigerfeldes (veraltete Version) vorgeführt:
Links und Download
Video | Online | Download (Mac) | Download (Win) | App Store
(leider ist die Online und Download-Versionen nur noch mit funktionierendem Flash-Plugin lauffähig)
Einige mögliche Aktivitäten und Aufgabenstellungen
Aufgaben legen
- Vorgegebene Aufgabe mit möglichst wenigen Klicks hinlegen und begründen (Ziel: geschickte Nutzung der Fünferportionen)
- Eine Zahlziffer abdecken, die Aufgabe hinlegen und die fehlende Stellen bestimmen. Die Lösung kann selbst kontrolliert werden, indem das Abdeckfeld wieder verschoben wird (evtl. auch als Partneraufgabe).
- offene, problemstrukturierte Aufgabenstellungen bearbeiten z.B. „Lege möglichst viele Aufgaben mit dem Ergebnis 12“.
- Aufgaben mit Zehnerübergang z.B. Zerlegungsanzeige zudecken, Zerlegung vom Schüler nennen („Wie lautet die Zerlegung über den Zehner“) lassen und dann durch Verschieben der Abdeckung kontrollieren.
Beziehungen zwischen Aufgaben entdecken
- Variationen an einer Aufgaben vornehmen und Auswirkungen beobachten z.B. Plättchen umdrehen, Eins/Fünf hinzufügen/wegnehmen etc.
- Variationen durchführen mit einer zugedeckten Zahlziffer – was passiert mit der Zahlziffer bei Manipulationen an den Plättchen am Zwanzigerfeld?
- Zehnerübergang – Wie verändert sich die Zerlegung des zweiten Summanden (blaue Plättchen), wenn die Anzahl roter Plättchen verändert wird?
- Offene Aufgaben z.B. – Finde und speichere möglichst viele Aufgaben mit dem Ergebnis 12?
Weitere Übungen und Hinweise zur Arbeit mit dem Zwanzigerfeld sind bei Wittmann & Müller (1994, S. 33ff.) aufgeführt.
Literatur
Wittmann, E. C. & Müller, G. N. (1994). Handbuch produktiver Rechenübungen. Band 1: Vom Einspluseins zum Einmaleins (2., überarb. Aufl.). Stuttgart: Klett.

Hallo Herr Urff,
benutze ihre Mathe Apps schon seit Jahren mit großem Erfolg bei den SchülerInnen.
Leider kann ich die Zwanzigerfeld App nun nicht mehr auf mein neueres iPhone laden, was früher ging…
Deg AppStore meldet immer „..derzeit in deiner Region o.ä. …nicht verfügbar…“
Haben Sie mir einen Rat?
Herzlichen Dank
Hallo Herr Urff,
benutze ihre Mathe Apps schon seit Jahren mit großem Erfolg bei den SchülerInnen.
Leider kann ich die Zwanzigerfeld App nun nicht mehr auf mein neueres iPhone laden, was früher ging…
Deg AppStore meldet immer „..derzeit in deiner Region o.ä. …nicht verfügbar…“
Haben Sie mir einen Rat?
Herzlichen Dank
Hallo,
ich bin gerade auf die Anwendung gestoßen. Wirklich sehr schön! Ich hätte noch ein paar Anregungen, die etwas weiter gehen und für gemeinsames Automatisieren der 20er Struktur gedacht wären:
Unterrichtssituation:
Die Kinder sollen möglichst schnell die Gesamtsumme der gelegten Punkte bestimmen und dabei die 5er-Struktur des 20er Feldes nutzen (müssen), ohne dabei zu zählen (bzw. zählen zu können).
Anregungen
Die Punkte lassen sich schwärzen, da blau und rot in diesem Fall nicht von Bedeutung sind. Teilsummen und Gesamtsumme lassen sich komplett ausblenden, um keine Zählmöglichkeit auf symbolischer Ebene zu geben. Das Feld lässt sich über ein Sechseck (z.B. erstellt über sechs Mausklicks) flexibel abdecken (z.B. so, dass im 20er Feld im unteren 10er nur das letze Plättchen der ersten 5er Bündelung zu sehen ist und der Rest demzufolge aufgefüllt sein muss).
Über eine Rückmeldung über etwaiges Realisierungsinteresse würde ich mich freuen. In jedem Fall probiere ich die Anwendung im Unterricht mal aus!
Noch eine letzte Frage meinerseits: Lässt sich das ganze auch offline nutzen (etwa als kleines Applet?)
[…] virtuelle Zwanzigerfeld hat eine Funktionserweiterung und kleine Detailverbesserungen erhalten. Neben neu gestalteten […]
[…] Plättchen weggestrichen (d.h. der Subtrahend vergrößert/verkleinert) werden. Über die von dem Zwanzigerfeld zur Addition bekannten Einfügefeldern lasst sich der Minuend verändern. Die sonstigen Funktionen sind ähnlich […]
Danke, Herr Wendt, für ihren Kommentar.
Minusrechnen ist in Vorbereitung und wird definitiv bald kommen.
Viele Grüße,
Christian Urff
Hallo! Absolut spitze wäre es als Aufgabengenerator, wenn man auch MINUSRECHNEN könnte. Dann wäre es perfekt.
Viele Grüße
Sascha Wendt
[…] virtuelle Zwanzigerfeld hat in der neusten Version ein kleines Schmankeln spendiert bekommen – eine interaktive […]
Vielen Dank, Frau Unterbeck, für ihre Anregung.
Ein Modus zur Darstellung der Plättchen untereinander in Reihen habe ich nun noch eingebaut (war sowieso in Planung). In der aktualisierten Fassung des Zwanzigerfeldes kann über den „Einstellungsknopf“ (zweites Symbol von links; das Symbol gefällt mir noch nicht so gut, vielleicht finde ich noch etwas passenderes) zwischen linearer und Reihendarstellung gewechselt werden. Somit sollte die Darstellung nun flexibler hinsichtlich der Veranschaulichung unterschiedlicher Rechenstrategien sein.
Es lässt sich übrigens immer auch manuell die Anordnung verändern (per Drag&Drop der Plättchen) und so weitere freie Anordnungen realisieren, was aber auf Dauer natürlich sehr mühsam ist.
Hallo, ich bin Grundschullehrerin und bin durch Zufall auf diese tolle Seite gestoßen.
Es wäre schön, wenn die Anordung im 20-er-Feld auch so funktionieren würde, dass die Zahlen auch untereinander aufleuchten würden und somit das Rechnen mit der „Kraft der 5“ beim Zehnerübergang dargestellt werden könnte.
Beipiel: 8+7=?
ooooo ooo 5+3=8
ooooo oo 5+2=7
5+5+3+2=15
Mit freundlichen Grüßen
Claudia Unterbeck
[…] virtuelle Hunderterfeld ist eine Erweiterung und Fortführung des virtuellen Zwanzigerfeldes. Im Unterschied zum virtuellen Zwanzigerfeld für die Addition im Zahlenraum bis Hundert geht es […]
[…] Das virtuelle Hunderterfeld ist eine Erweiterung und Fortführung des virtuellen Zwanzigerfeldes. […]