Blitzblick-Übungen sind in vielen Lernsoftware-Paketen enthalten. Solche Übungen lassen sich gut mit dem Computer realisieren, weil der Computer zeitgesteuert Mengenbilder ein- und ausblenden lassen kann (dynamische Anzeige von Repräsentationen). Deshalb habe ich mir einige Realisierungen von Blitzblick-Übungen mit dem Computer genauer angesehen. Zuvor erläutere ich noch kurz, warum Blitzblick-Übungen für die Förderung mathematischer Kompetenzen bedeutsam sind.
Warum Blitzblick-Übungen?
Die Fähigkeit, kleine Anzahlen sehr schnell und ohne Abzählen zu erfassen (Simultanerfassung, perzeptuelles Subitizing, vgl. Clements 1999) ist angeboren und ist eine zentrale vorbegriffliche Grundlage für die Entwicklung eines mathematischen Verständnisses für Mengen und Zahlen (Dehaene 1999, 66). Diese spontane Fähigkeit, nichtzählend eine kleine Anzahl (normalerweise 3-4 Elemente) ohne numerisches Wissen wiederzuerkennen, ermöglicht es uns, zählbare Einheiten voneinander zu unterscheiden.
Darauf aufbauend, gibt es noch einen zweiten Typ der Simultanerfassung, die sogenannte quasi-simultane Mengenerfassung (Gerster & Schulz 2003, 337; oder auch konzeptuelle Subitizing, vgl. Clements 1999). Damit ist gemeint, dass eine Menge zugleich als Ganzes und als Zusammensetzung unterschiedlicher Teile identifiziert wird. Dadurch können – aufbauend auf dem perzeputellen Subitizing – auch größere Anzahlen schnell erfasst werden, indem einzelne Mengengruppen zu einer Gesamtmenge zusammengesetzt werden. Diese Fähigkeit spielt für arithmetische Kompetenzen eine bedeutsame Rolle, weil damit eine Erfassung von Quantitäten nach dem Teile-Ganzes-Konzept (eine Menge lässt sich in Teilmengen zerlegen und daraus wieder zusammensetzen) angebahnt wird und dies die konzeptuelle Basis für die Entwicklung nicht-zählender Rechenstrategien bei den Grundoperationen darstellt (vgl. Gerster & Schulz2003, 337ff.).
Studien bei älteren Schülern untermauern die Bedeutung von Subitzing für die Entwicklung mathematischer Kompetenzen und die schulische Leistung (Schäfer 2005; Fischer 2003). Schüler mit Entwicklungsverzögerungen bei der Simultanerfassung benötigen wesentlich mehr Zeit für die strukturierte Erfassung größerer Anzahlen, weil sie in kleinere Teilmengen untergliedern müssen oder die Menge abzählen. Viele strukturierte didaktische Materialien lassen sich dann nicht mehr effizient (d.h. nicht-zählend) nutzen, da sie auf der Fähigkeit zur strukturierten Mengenerfassung aufbauen (Bsp: Zwanzigerfeld, Hunderterfeld, Rechenbrett usw.). Fischer (2003) konnte nachweisen, dass sich die Fähigkeit zur Erfassung kleiner Mengen als auch zur Erfassung von Mustern gezielt trainieren lassen und diese Trainingseffekte eine nachhaltige Auswirkung auf die Rechenleistungen der Schüler haben. Dazu werden Blitzblick-Übungen empfohlen, bei denen den Kindern nur sehr kurz – so dass ein Abzählen nicht möglich ist – Mengenbilder gezeigt werden und sie diese ohne Abzählen bestimmen müssen.
Realisierungsformen von Blitzblickübungen
Blitzblickübungen beeinhalten grundsätzlich folgende Elemente, die in ihrer Ausprägungsform variiert werden können:
- Zahlenraum der dargestellten Menge (bis 5, 10, 20, 100)
- Strukturierung der Mengenbilder (unstrukturiert, Würfelbilder, linear strukturiert in Fünferportionen, im Zehnerfeld/Zwanzigerfeld/Hunderterfeld, etc.)
- Verwendete Mengenelemente (Plättchen, Finger, Geldstücke, Würfelbilder, etc.)
- Blitzblick-Dauer (d.h. die Zeit, in der das Mengenbild zu sehen ist)
- Hilfestellungen (z.B. Wiederholung der Anzeige, Verlängerung der Blitzblickdauer, gestufte Hilfestellung etc.)
Aus eigenen Beobachtungen von Kindern bei der Arbeit mit Blitzblickübungen (Urff 2010) hat sich gezeigt, dass folgende Realisierungsaspekte besonders zu bedeutsam sind:
- Die Zeitdauer sollte flexibel einstellbar sein, weil gerade zählende Rechner sehr schnell im Abzählen sind und es bei kleinen Mengen und hinreichend langer Blitzblickdauer schaffen, die Menge (evtl. noch mit Hilfe ihres visuellen Gedächtnisses) zu zählen.
- Gerade Kinder mit Schwierigkeiten (die Mengen vorwiegend zählend bestimmen) entwickeln häufig „Kompensationsstrategien“ für die Bestimmung der Menge, indem sie gezielt die Hilfestellungen des Programms „ausnutzen“ um Mengenbilder wiederholt angezeigt zu bekommen. Dazu wird beispielsweise zunächst irgendeine (geschätzte) Zahl eingeben. Viele Programme zeigen daraufhin das Mengenbild nocheinmal (länger) an, was dann meist zum Abzählen/Weiterzählen reicht. Die Rückmeldung/Hilfe des Programms sollte also so gestaltet sein, dass sie sich nicht für die Erhöhung der Blitzblickdauer und damit leicht für eine zählende Erfassung der Menge ausnutzen lassen. Stattdessen haben sich strategische Hinweise und Hilfen für die Mengenerfassung (z.B. Hinweis/Hervorhebungen auf Strukturen/Orientierungspunkte der Mengenbilder) als hilfreicher erwiesen und führten zur Verbesserung der quasi-simultanen Erfassung der Mengenbilder.
- Kinder dürfen nicht ohne Vorbereitung auf (computergestützte) Blitzblick-Übungen losgelassen werden. Gemeinsam sollten zuvor einige Übungen bearbeitet werden und dabei individuelle Strategien zur schnellen/effizienten Bestimmung der Mengen ausgetauscht und besprochen werden. Kinder können strukturierte Mengen erst quasi-simultan erfassen, wenn sie über Strategien verfügen, wie Muster und Mengenportionen schnell erkannt werden können. Insbesondere sollte deshalb die Erkennung bestimmter Muster, vor allem in unter Beachtung der Beziehungen zu Fünferportionen (Kraft der Fünf) eine zentrale Voraussetzung (vgl. Krauthausen 1995, Gerster 1996).
Beispiele
Die Lernsoftware „Blitzrechnen“ bietet mit der Übung „Wie viele?“ eine Übung zum Blitzblick für die 1. und 2. Klasse an. Je nach Klassenstufe wird hier die Erfassung von unterschiedlich strukturierten Mengen bis 10 oder bis 100 (im Hunderterfeld) geübt.

Bei meinen Beobachtungen stellte sich als Nachteil heraus, dass die Blitzblickdauer fest eingestellt ist und bei einem Fehler oder dem erneuten Drücken der Returntaste das Mengenbild nochmal deutlich länger angezeigt wird. Schüler, die Schwierigkeiten bei der Erfassung der Mengen hatten, fanden diese „Funktion“ des Programms schnell heraus und nutzen die Hilfestellung gezielt aus, um das Bild nochmal zu sehen und zählend die Mengen zu bestimmen.
„Mathematikus“ beinhaltet eine Übung zur Simultanerfassung von Mengen am Zwanzigerfeld. Diese strukturierte Mengendarstellung wechselt mit der Zeit (und Schwierigkeit) auf eine lineare Darstellungsform um, wobei eine Fünferstrukturierung (Kraft der Fünf) beibehalten bleibt. Die Blitzblickdauer ist zunächst recht kurz, wird nach dem ersten Fehlversuch jedoch etwas länger.
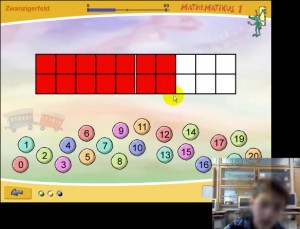
Positiv aufgefallen im Einsatz ist die Realisierung der gestuften Hilfestellung. Wird eine die Menge mehrfach falsch erkannt, erscheint eine visuelle Hilfestellung und der Hinweis auf die Fünferstrukturierung. Den Schüler hilft dieser gezielte Hinweis auf eine effektive Vorgehensweise bei der schnelleren Erfassung der Menge oftmals weiter und ermöglicht eine Fehlerkorrektur und die Entwicklung effizienter Mustererkennungsstrategien.
Im „Rekenweb“ findet sich auch eine Blitzblick-Übung (Speedy Pictures), die ich bereits in einem anderen Artikel vorgestellt habe. Besonders fällt an dieser Übung die große Auswahl an Einstellungsparameter und Veranschaulichungsmittel (Finger, Würfelbilder, Rechenschieber, Zehnerfeld, Geld) auf.

Außer, dass das Applett sehr klein ausgefallen ist, finde ich die Umsetzung sehr gelungen. Zudem ist das Lernmodul kostenlos übers Internet abrufbar und in jedem Browser dank Java lauffähig. Es wird durch die Farbe der Punkte (rot=falsch, grün=richtig) angezeigt, ob die eingegebene Lösung richtig war.
Etwas anders als die anderen Übungen ist der Blitzblick-Modus in der Lernsoftware „Mathe-Hilfe“ des Eugen-Traeger-Verlags. Sämtliche Rechenübungen lassen sich hier in einem Blitzblickmodus darstellen, d.h. die Aufgabe wird dann nur kurzzeitig in strukturierter Form (je nach Zahlenraum im Zwanziger- oder Hunderterfeld) eingeblendet.Aus diesem kurzen Mengenbild (im Zwanziger- oder Hunderterfeld) müssen die Mengen oder Rechenaufgaben (es gibt sowohl Plus als auch Minusaufgaben) notiert werden. Auch in diesem Programm lässt sich das Mengenbild über eine Button wiederholt anzeigen.
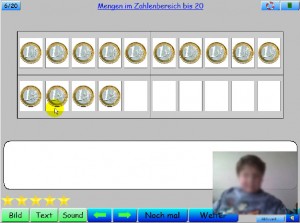
In der Grundeinstellung ist die Blitzblickdauer recht hoch eingestellt, so dass schnelle Zähler ohne Probleme die Menge abzählen können. Die Blitzblickdauer lässt sich jedoch in den Einstellungen verändern. Positiv ist die Vielfalt und Stufung der angebotenen Aufgaben. So lassen sich sehr differenziert Aufgabenfolgen mit unterschiedlichen Schwierigkeitsgraden auswählen, die bis 10, zehnerüberschreitend, zwischen 10 und 20 oder bis 1000 sind und zwischen dem schnellen Erfassen von Mengenbilder, Plusaufgaben, Minusaufgaben auswählen. Auch eigene Blitzblick-Übungsaufgaben lassen sich über einen Texteditor einarbeiten.
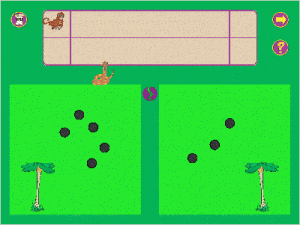
Blitzblickübungen finden sich auch noch in dem Rechenspiel „Das Zahlenrennen“ (kostenloser Download). Hier muss schneller als ein Computergegner die größere von zwei Mengen erkannt bzw. bestimmt werden, wobei die Blitzblickdauer (bzw. die Schnelligkeit des Computergegners) hier adaptiv eingestellt wird. Dadurch bleibt die Spielspannung erhalten. Dies funktionierte bei meinen Nutzungsbeobachtungen sehr gut. Allerdings hat das Lernspiel auch einen nicht unproblematischen Gestaltungsaspekt: Bei der anschließenden Übertragung der erkannten Mengen auf das Spielfeld wird durch die Gestaltung eine zählende Übertragung der Menge in Einzelportionen nahegelegt.
Weitere Blitzblickübungen
In dem Lernpaket Kostis-Mathe sind auch Blitzblickübungen enthalten.
Quellenangaben
Clements, D. H. (1999): Subitizing: What is it? Why teach it? In: Teaching Children Mathematics, 5 (7), S. 400-405.
Dehaene, S. (1999). Der Zahlensinn oder warum wir rechnen können. Birkhäuser Verlag.
Fischer, B. (2003). Hören – Sehen – Blicken – Zählen: Teilleistungen und ihre Störungen. Bern: Huber.
Fischer, B. & Schäfer, J. (2002): Die Entwicklung der Simultanerfassung bei Rechenschwäche. In: Die Akzente, 57 (3), S. 50-52.
Gerster, H.-D. & Schultz, R. (2003). Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht. Freiburg: Pädagogische Hochschule.
Gerster, H.-D. (1996): Vom Fingerrechnen zum Kopfrechnen – Methodische Schritte aus der Sackgasse des zählenden Rechnen. In: G. Eberle & R. Kornmann (Hrsg.): Lernschwierigkeiten und Vermittlungsprobleme im Mathematikunterricht an Grund- und Sonderschulen. Weinheim: Deutscher Studienverlag. S. 137-162.
Krauthausen, G. (1995): Die „Kraft der Fünf“ und das denkende Rechnen. In: G. N. Müller & E. C. Wittmann (Hrsg.): Mit Kindern rechnen. Frankfurt am Main: Arbeitskreis Grundschule. S. 87-108.
Schäfer, J. (2005). Rechenschwäche in der Eingangsstufe der Hauptschule. Lernstand, Einstellungen und Wahrnehmungsleistungen. Eine empirische Studie. Hamburg: Kovac.
Urff, C. (2010). Computergestützte Förderung grundlegender mathematischer Kompetenzen – Theoretische Analysen zu Mehrwertpotentialen digitaler Lernmedien und empirische Fallstudien zu Lernprozessen bei der Nutzung aktueller mathematischer Lernsoftware von Schülern mit besonderem Förderbedarf. Dissertation an der PH Ludwigsburg (Fakultät für Sonderpädagogik) in Vorbereitung.

[…] Pictures: Hier geht es darum, Mengen bis 10 oder 20 per “Blitzblick” möglichst schnell zu erfassen. Die Mengendarstellung kann dabei als Fingerbilder, […]